Sicuramente con le estensioni spatial della quasi totalità degli rdbms in circolazione, l’utilizzo dei QuadTree e di sistemi proprietari per il posizionamento e l’interrogazione spaziale di insiemi di coordinate e oggetti, potrebbe risultare obsoleto. In realtà ci sono ancora tantissimi casi e campi di applicazione in cui risultano fondamentali, come lo sviluppo di applicazioni pda, giochi, e tutti quei casi in cui non sia possibile utilizzare un database sql.
Essendomi trovato nell’ultimo caso descritto per motivi di lavoro e forte dell’esperienza nello sviluppo di prototipi di videogames acquisita per hobby negli anni passati, ho adottato questa soluzione per un applicazione web in cui era fondamentale fare delle query spaziali su un insieme di punti (descritti da longitudine e latitudine), per geolocalizzare dei punti di interesse intorno alla mia posizione entro un certo raggio, presi da dei file xml.
Per facilità e velocità mi sono basato sull’articolo scritto da Michael Coyle su CodeProject.com:
http://www.codeproject.com/KB/recipes/QuadTree.aspx
Un QuadTree è un modo di ripartire lo spazio e facilitare le query su sistemi 2D, molto utilizzato nei GIS in generale, o nella gestione della posizione degli oggetti nei videogames.
Il QuadTree è apppunto un albero formato da quadrati. Lo spazio viene ripartito in regioni quadrate suddivise in 4 quadranti ,partendo dalla regione che contiene tutto fino al livello minimo da noi definito, in maniera ricorsiva. Quindi ogni quadrante viene poi ulteriormente suddiviso.
Per eseguire delle query su un quadtree basta poi effettuare il traversing dell’albero ed eseguire delle semplici intersezioni per capire quali oggetti sono posizionati all’interno di una determinata regione (che è l’input della ricerca).
Questo permette di eseguire ricerche molto veloci su insiemi statici di coordinate. Ovviamente è un albero statico, che nell’algoritmo cosi come proposto non permette un dinamismo nella gestione delle regioni I(in quanto andrebbe ricalcolata la struttura ad ogni modifica), ma è molto semplice da realizzare, ed il punto di partenza fondamentale è conoscere i confini dell’area che andremo a gestire..
Nel mio caso dovendo rappresentare dei punti di interesse sparsi sul suolo italiano, ho acquisito il punto centrale dell’italia e calcolato un quadrato che la contenesse tutta, e poi ho trasformato le coordinate geografiche in coordinate 2d, utilizzando gli stessi algoritmi di google maps, quindi con il fattore di zoom e tutto il resto.
Questa è la funzione che ho usato per la conversione di coordinate geografiche in coordinate schermo (x,y):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| public static PointF Geographical2Screen(Position position)
{
//converte le coordinate in pixel
float x;
float y;
double xD = (position.Longitude - mapLongitude) / resolution;
double yD = Math.Log(Math.Tan(Math.PI * (0.25 + position.Latitude / 360))) * u180dPiResolution;
x = Convert.ToSingle(xD + viewWidthHalf);
y = Convert.ToSingle((y0 - yD) + viewHeightHalf);
return new PointF(x, y);
} |
dove per costanti ho usato, ipotizzando di inscrivere tutta l’area in un quadrato di 1024 pixel per 1024 pixel e usato un fattore di zoom che mi permettesse di mantenere tutta la mappa d’italia in questo quadrato .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| public static float WIDTH = 1024F;
public static float HEIGHT = WIDTH;
public static float CENTERMAP = WIDTH /2;
public static float TOTALPIXEL = WIDTH;
public static int zoom = 6;
public static double resolution = 360.0 / (Math.Pow(2,zoom) * 256);
public static double u180dPiResolution = 40.7436654315252 * Math.Pow(2, zoom);
public static double mapLatitude = 41.8719400F;
public static double mapLongitude = 12.5673800F;
public static double y0 = Math.Log(Math.Tan(Math.PI * (0.25 + mapLatitude / 360))) * u180dPiResolution;
public static float viewWidthHalf = WIDTH / 2.0f;
public static float viewHeightHalf = HEIGHT / 2.0f; |
Fatto questo, ho costruito il mio quadtree a partire dal nodo principale:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| public class QuadTree
{
QuadTreeNode m_root;
RectangleF m_rectangle;
//solo per funzionalita di paint
public delegate void QTAction(QuadTreeNode obj);
public QuadTree(RectangleF rectangle)
{
m_rectangle = rectangle;
m_root = new QuadTreeNode(m_rectangle);
}
public int Count { get { return m_root.Count; } }
public void Insert(IQuadPoint item)
{
m_root.Insert(item);
}
public ListQuery(RectangleF area)
{
return m_root.Query(area);
}
public void ForEach(QTAction action)
{
m_root.ForEach(action);
}
} |
Il delegato QTAction viene usato per poter rappresentare ad esempio tramite delle paint i nodi e i quad nel viewer.(un callback per il traversing, e per ogni elemento, disegno..)
il punto definito come risultato e’ un interfaccia da me cosi definita e che serve a markare gli oggetti che avranno la possibilità di essere inseriti nella struttura (per i fini della ricerca l’importante che l’oggetto da trovare abbia una posizione X,Y)
1
2
3
4
| public interface IQuadPoint
{
PointF Point { get; }
} |
Fatto questo passo alla definizione del nodo del quad, dove risiede l’implementazione ricorsiva della ricerca:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
| public class QuadTreeNode
{
//area occupata da questo nodo
RectangleF m_bounds;
//contenuto del nodo
List m_contents = new List();
//figli di questo nodo
List m_nodes = new List(4);
static int maxElements = 50;
static int minSize = 10;
public QuadTreeNode(RectangleF bounds)
{
m_bounds = bounds;
}
//test se vuoto
public bool IsEmpty { get { return (m_bounds.IsEmpty || m_nodes.Count == 0) && m_contents.Count==0; } }
//confini del nodo
public RectangleF Bounds { get { return m_bounds; } }
//contenuto del nodo
public List Contents { get { return m_contents; } }
//count degli item del nodo e dei subNodi
public int Count
{
get
{
int count = 0;
foreach (QuadTreeNode node in m_nodes)
count += node.Count;
count += this.Contents.Count;
return count;
}
}
//ritorna il contenuto globale di questo nodo(questo + subNodi)
public List FullContents
{
get
{
List results = new List();
foreach (QuadTreeNode node in m_nodes)
results.AddRange(node.FullContents);
results.AddRange(this.Contents);
return results;
}
}
//ritorna gli item all'interno di una certa area
public List Query(RectangleF queryArea)
{
List results = new List();
foreach (IQuadPoint item in this.Contents)
{
if (queryArea.Contains(item.Point))
results.Add(item);
}
foreach (QuadTreeNode node in m_nodes)
{
if (node.IsEmpty)
continue;
//se un subNodo contiente completamente la query area.. prendi tutto e esci
if (node.Bounds.Contains(queryArea))
{
results.AddRange(node.Query(queryArea));
break;
}
//se l'area contiene il subnodo, lo importa tutto e continua
if (queryArea.Contains(node.Bounds))
{
results.AddRange(node.FullContents);
continue;
}
//se il subnodo interseziona l'area di ricerca, allora inoltra la query ai suoi subNodi
if (node.Bounds.IntersectsWith(queryArea))
{
results.AddRange(node.Query(queryArea));
}
}
return results;
}
//inserisce un item
public void Insert(IQuadPoint item)
{
if (!m_bounds.Contains(item.Point))
{
//System.Diagnostics.Debug.Print("punto non compreso nel nodo:");
// System.Diagnostics.Debug.Print("--->"+item.Point);
return;
}
//se c'e' capienza e non ho generato le foglie
if (this.Contents.Count < maxElements && m_nodes.Count ==0) { //inserisco in questo this.Contents.Add(item); return; } else { //genera i subtree if (m_nodes.Count == 0) { CreateSubNodes(); if (m_nodes.Count > 0)
{
//ridistribuisco sui figli
foreach (IQuadPoint punto in Contents)
{
foreach (QuadTreeNode node in m_nodes)
{
if (node.Bounds.Contains(punto.Point))
{
node.Insert(punto);
break;
}
}
}
Contents.Clear();
}
else
{
//forza inserimento in questo nodo indipendentemente dalla size:
this.Contents.Add(item);
}
}
//per ogni subnodo fa l'add ricorsivo fino ad arrivare al quad piu piccolo
foreach (QuadTreeNode node in m_nodes)
{
if (node.Bounds.Contains(item.Point))
{
node.Insert(item);
return;
}
}
}
}
//solo in caso di paint
public void ForEach(QuadTree.QTAction action)
{
action(this);
// draw the child quads
foreach (QuadTreeNode node in this.m_nodes)
node.ForEach(action);
}
//Crea i subNodi
private void CreateSubNodes()
{
// the smallest subnode has an area
if ((m_bounds.Height * m_bounds.Width) return;
float halfWidth = (m_bounds.Width / 2f);
float halfHeight = (m_bounds.Height / 2f);
m_nodes.Add(new QuadTreeNode(new RectangleF(m_bounds.Location, new SizeF(halfWidth, halfHeight))));
m_nodes.Add(new QuadTreeNode(new RectangleF(new PointF(m_bounds.Left, m_bounds.Top + halfHeight), new SizeF(halfWidth, halfHeight))));
m_nodes.Add(new QuadTreeNode(new RectangleF(new PointF(m_bounds.Left + halfWidth, m_bounds.Top), new SizeF(halfWidth, halfHeight))));
m_nodes.Add(new QuadTreeNode(new RectangleF(new PointF(m_bounds.Left + halfWidth, m_bounds.Top + halfHeight), new SizeF(halfWidth, halfHeight))));
}
} |
Fatto cio è possibile usare il QuadTree e inserire i nostri oggetti.
Seguendo il progetto di Michael Coyle, ho realizzato un piccolo viewer per controllare il risultato e fare delle query di prova , il sistema è molto veloce in fase di inserimento (40000 punti inseriti in un secondo comprensivo di generazione di tutti i quad), e tempi di risposta in caso di interrogazione molto bassi, sotto il millisecondo.
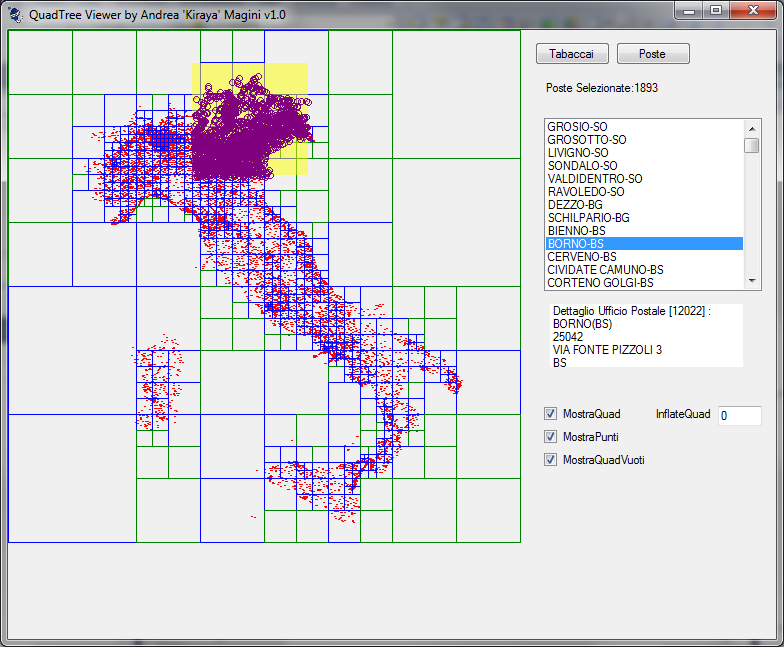
Ovviamente per interrogare il quad, bisogna trasformare le coordinate geografiche in coordinate 2d piane.
Le formule di intersezione sono eseguite utilizzando le System.Drawing, beneficiando cosi della velocità delle librerie grafiche di windows.